RNN Language Models¶
0. Introduction¶
The language model is modeling the probability of generating natural language sentences or documents. You can use the language model to estimate how natural a sentence or a document is. Also, with the language model, you can generate new sentences or documents.
Let’s start with modeling the probability of generating sentences. We represent a sentence as \({\bf X} = ({\bf x}_0, {\bf x}_1, ..., {\bf x}_T)\), in which \({\bf x}_t\) is a one-hot vector. Generally, \({\bf x}_0\) is the one-hot vector of BOS (beginning of sentence), and \({\bf x}_T\) is that of EOS (end of sentence).
A language model models the probability of a word occurrence under the condition of its previous words in a sentence. Let \({\bf X}_{[i, j]}\) be \(({\bf x}_i, {\bf x}_{i+1}, ..., {\bf x}_j)\), the occurrence probability of sentence \(\bf X\) can be represented as follows:
So, the language model \(P({\bf X})\) can be decomposed into word probabilities conditioned with its previous words. In this tutorial, we model \(P({\bf x}_t|{\bf X}_{[0, t-1]})\) with a recurrent neural network to obtain a language model \(P({\bf X})\).
1. Basic Idea of Recurrent Neural Net Language Model¶
1.1 Recurrent Neural Net Language Model¶
Recurrent Neural Net Language Model (RNNLM) is a type of neural net language models which contains the RNNs in the network. Since an RNN can deal with the variable length inputs, it is suitable for modeling the sequential data such as sentences in natural language.
We show one layer of an RNNLM with these parameters.
Symbol |
Definition |
|---|---|
\({\bf x}_t\) |
the one-hot vector of \(t\)-th word |
\({\bf y}_t\) |
the \(t\)-th output |
\({\bf h}_t^{(i)}\) |
the \(t\)-th hidden layer of \(i\)-th layer |
\({\bf p}_t\) |
the next word’s probability of \(t\)-th word |
\({\bf E}\) |
Embedding matrix |
\({\bf W}_h\) |
Hidden layer matrix |
\({\bf W}_o\) |
Output layer matrix |
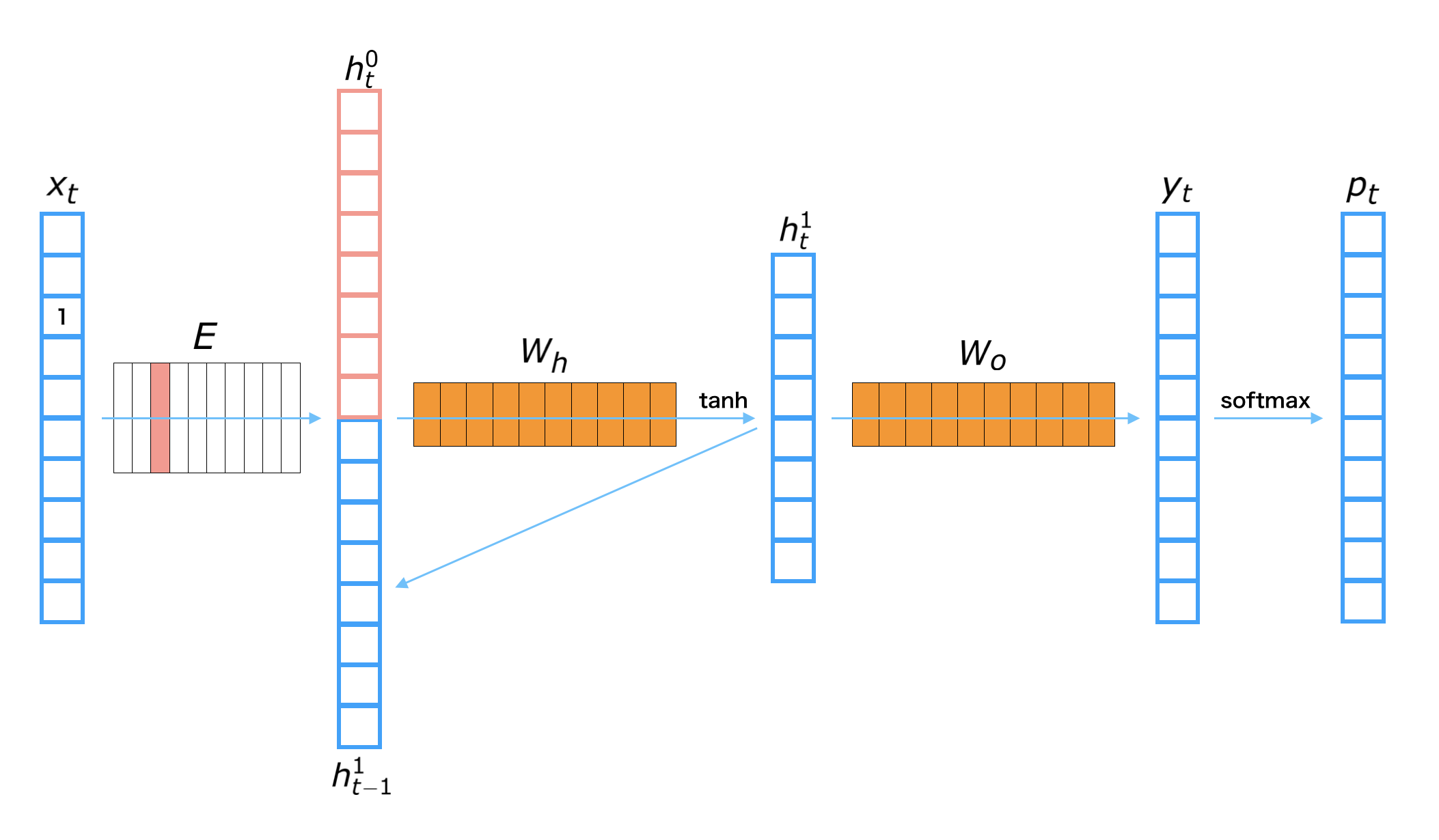
The process to get a next word prediction from \(i\)-th input word \({\bf x}_t\)¶
Get the embedding vector: \({\bf h}_t^{(0)} = {\bf E} {\bf x}_t\)
Calculate the hidden layer: \({\bf h}_t^{(1)} = {\rm tanh} \left( {\bf W}_h \left[ \begin{array}{cc} {\bf h}_t^{(0)} \\ {\bf h}_{t-1}^{(1)} \end{array} \right] \right)\)
Calculate the output layer: \({\bf y}_t = {\bf W}_o {\bf h}_t^{(1)}\)
Transform to probability: \({\bf p}_t = {\rm softmax}({\bf y}_t)\)
Note
Note that \(\rm tanh\) in the above equation is applied to the input vector in element-wise manner.
Note that \(\left[ \begin{array}{cc} {\bf a} \\ {\bf b} \end{array} \right]\) denotes a concatenated vector of \({\bf a}\) and \({\bf b}\).
Note that \({\rm softmax}\) in the above equation converts an arbitrary real vector to a probability vector which the summation over all elements is \(1\).
1.2 Perplexity (Evaluation of the language model)¶
Perplexity is the common evaluation metric for a language model. Generally, it measures how well the proposed probability model \(P_{\rm model}({\bf X})\) represents the target data \(P^*({\bf X})\). Let a validation dataset be \(D = \{{\bf X}^{(n)}\}_{n=1}^{|D|}\), which is a set of sentences, where the \(n\)-th sentence length is \(T^{(n)}\), and the vocabulary size of this dataset is \(|\mathcal{V}|\), the perplexity is represented as follows:
We usually use \(b = 2\) or \(b = e\). The perplexity shows how much varied the predicted distribution for the next word is. When a language model represents the dataset well, it should show a high probability only for the correct next word, so that the entropy should be high. In the above equation, the sign is reversed, so that smaller perplexity means better model.
During training, we minimize the below cross entropy:
where \(\hat P\) is the empirical distribution of a sequence in the training dataset.
2. Implementation of Recurrent Neural Net Language Model¶
There is an example of RNN language model in the official repository, so we will explain how to implement a RNNLM in Chainer based on that: examples/ptb
2.1 Model Overview¶
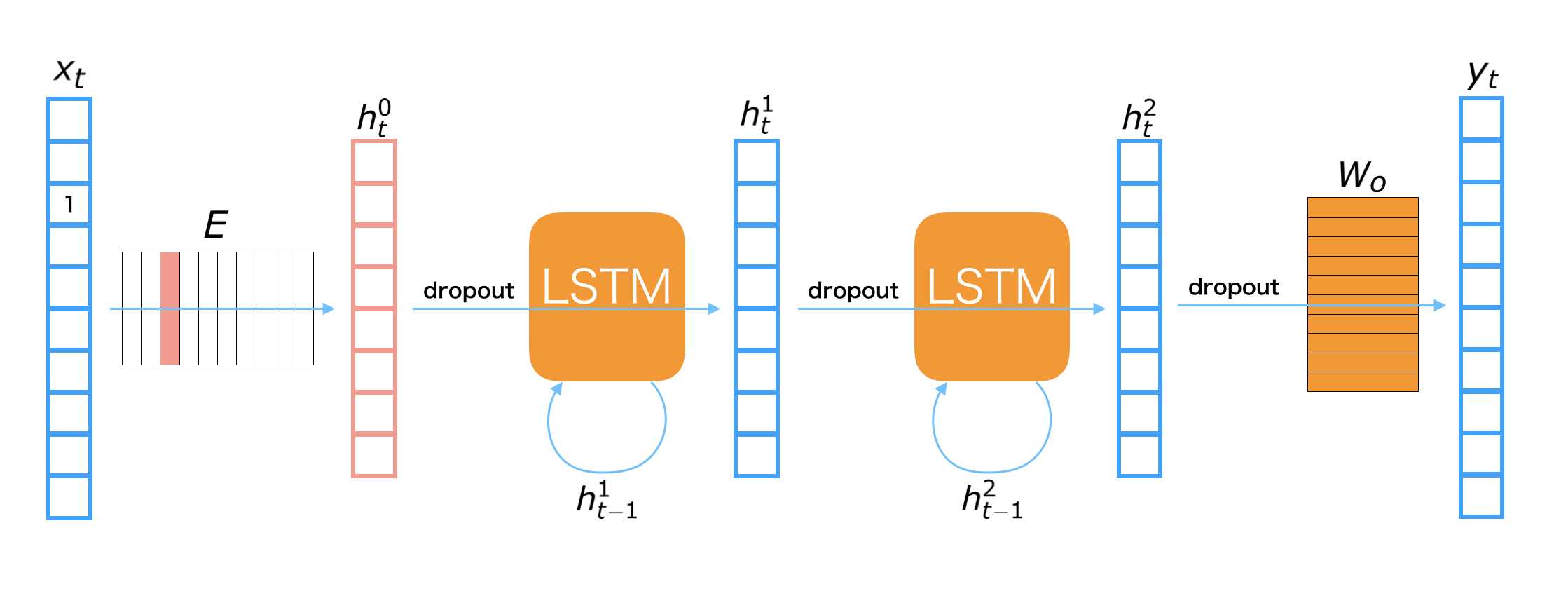
The RNNLM used in this notebook is depicted in the above figure. The symbols appeared in the figure are defined as follows:
Symbol |
Definition |
|---|---|
\({\bf x}_t\) |
the one-hot vector of \(t\)-th word |
\({\bf y}_t\) |
the \(t\)-th output |
\({\bf h}_t^{(i)}\) |
the \(t\)-th hidden layer of \(i\)-th layer |
\({\bf p}_t\) |
the next word’s probability of \(t\)-th word |
\({\bf E}\) |
Embedding matrix |
\({\bf W}_h\) |
Hidden layer matrix |
\({\bf W}_o\) |
Output layer matrix |
LSTMs (long short-term memory) are used for the connection of hidden layers. A LSTM is one of major recurrent neural net modules. It is designed for remembering the long-term memory, so that it should be able to consider relationships of distant words, such that a word at beginning of sentence and it at the end. We also use Dropout before both LSTMs and linear transformations. Dropout is one of regularization techniques for preventing overfitting on training dataset.
2.2 Step-by-step Implementation¶
2.2.1 Import Package¶
First, let’s import necessary packages.
"""
from __future__ import division
import argparse
import sys
import numpy as np
2.2.2 Define Training Settings¶
Define all training settings here.
parser.add_argument('--batchsize', '-b', type=int, default=20,
help='Number of examples in each mini-batch')
parser.add_argument('--bproplen', '-l', type=int, default=35,
help='Number of words in each mini-batch '
'(= length of truncated BPTT)')
parser.add_argument('--epoch', '-e', type=int, default=39,
help='Number of sweeps over the dataset to train')
parser.add_argument('--device', '-d', type=str, default='-1',
help='Device specifier. Either ChainerX device '
'specifier or an integer. If non-negative integer, '
'CuPy arrays with specified device id are used. If '
'negative integer, NumPy arrays are used')
parser.add_argument('--gradclip', '-c', type=float, default=5,
help='Gradient norm threshold to clip')
parser.add_argument('--out', '-o', default='result',
help='Directory to output the result')
parser.add_argument('--resume', '-r', type=str,
help='Resume the training from snapshot')
parser.add_argument('--test', action='store_true',
help='Use tiny datasets for quick tests')
parser.set_defaults(test=False)
parser.add_argument('--unit', '-u', type=int, default=650,
help='Number of LSTM units in each layer')
parser.add_argument('--model', '-m', default='model.npz',
help='Model file name to serialize')
2.2.3 Define Network Structure¶
An RNNLM written in Chainer is shown below. It implements the model depicted in the above figure.
class RNNForLM(chainer.Chain):
def __init__(self, n_vocab, n_units):
super(RNNForLM, self).__init__()
with self.init_scope():
self.embed = L.EmbedID(n_vocab, n_units)
self.l1 = L.LSTM(n_units, n_units)
self.l2 = L.LSTM(n_units, n_units)
self.l3 = L.Linear(n_units, n_vocab)
for param in self.params():
param.array[...] = np.random.uniform(-0.1, 0.1, param.shape)
def reset_state(self):
self.l1.reset_state()
self.l2.reset_state()
def forward(self, x):
h0 = self.embed(x)
h1 = self.l1(F.dropout(h0))
h2 = self.l2(F.dropout(h1))
y = self.l3(F.dropout(h2))
return y
When we instantiate this class for making a model, we give the vocabulary size to
n_vocaband the size of hidden vectors ton_units.This network uses
chainer.links.LSTM,chainer.links.Linear, andchainer.functions.dropoutas its building blocks. All the layers are registered and initialized in the context withself.init_scope().You can access all the parameters in those layers by calling
self.params().In the constructor, it initializes all parameters with values sampled from a uniform distribution \(U(-1, 1)\).
The
forwardmethod takes an word IDx, and calculates the word probability vector for the next word by forwarding it through the network, and returns the output.Note that the word ID
xis automatically converted to a \(|\mathcal{V}|\)-dimensional one-hot vector and then multiplied with the input embedding matrix inself.embed(x)to obtain an embed vectorh0at the first line offorward.
2.2.4 Load the Penn Tree Bank Long Word Sequence Dataset¶
In this notebook, we use Penn Tree Bank dataset that contains number of sentences.
Chainer provides an utility function to obtain this dataset from server and convert
it to a long single sequence of word IDs. chainer.datasets.get_ptb_words()
actually returns three separated datasets which are for train, validation, and test.
Let’s download and make dataset objects using it:
# Load the Penn Tree Bank long word sequence dataset
train, val, test = chainer.datasets.get_ptb_words()
2.2.5 Define Iterator for Making a Mini-batch from the Dataset¶
Dataset iterator creates a mini-batch of couple of words at different positions, namely, pairs of current word and its next word. Each example is a part of sentences starting from different offsets equally spaced within the whole sequence.
class ParallelSequentialIterator(chainer.dataset.Iterator):
def __init__(self, dataset, batch_size, repeat=True):
super(ParallelSequentialIterator, self).__init__()
self.dataset = dataset
self.batch_size = batch_size # batch size
self.repeat = repeat
length = len(dataset)
# Offsets maintain the position of each sequence in the mini-batch.
self.offsets = [i * length // batch_size for i in range(batch_size)]
self.reset()
def reset(self):
# Number of completed sweeps over the dataset. In this case, it is
# incremented if every word is visited at least once after the last
# increment.
self.epoch = 0
# True if the epoch is incremented at the last iteration.
self.is_new_epoch = False
# NOTE: this is not a count of parameter updates. It is just a count of
# calls of ``__next__``.
self.iteration = 0
# use -1 instead of None internally
self._previous_epoch_detail = -1.
def __next__(self):
# This iterator returns a list representing a mini-batch. Each item
# indicates a different position in the original sequence. Each item is
# represented by a pair of two word IDs. The first word is at the
# "current" position, while the second word at the next position.
# At each iteration, the iteration count is incremented, which pushes
# forward the "current" position.
length = len(self.dataset)
if not self.repeat and self.iteration * self.batch_size >= length:
# If not self.repeat, this iterator stops at the end of the first
# epoch (i.e., when all words are visited once).
raise StopIteration
cur_words = self.get_words()
self._previous_epoch_detail = self.epoch_detail
self.iteration += 1
next_words = self.get_words()
epoch = self.iteration * self.batch_size // length
self.is_new_epoch = self.epoch < epoch
if self.is_new_epoch:
self.epoch = epoch
return list(zip(cur_words, next_words))
@property
def epoch_detail(self):
# Floating point version of epoch.
return self.iteration * self.batch_size / len(self.dataset)
@property
def previous_epoch_detail(self):
if self._previous_epoch_detail < 0:
return None
return self._previous_epoch_detail
def get_words(self):
# It returns a list of current words.
return [self.dataset[(offset + self.iteration) % len(self.dataset)]
for offset in self.offsets]
def serialize(self, serializer):
# It is important to serialize the state to be recovered on resume.
self.iteration = serializer('iteration', self.iteration)
self.epoch = serializer('epoch', self.epoch)
try:
self._previous_epoch_detail = serializer(
'previous_epoch_detail', self._previous_epoch_detail)
except KeyError:
# guess previous_epoch_detail for older version
self._previous_epoch_detail = self.epoch + \
(self.current_position - self.batch_size) / len(self.dataset)
if self.epoch_detail > 0:
self._previous_epoch_detail = max(
self._previous_epoch_detail, 0.)
else:
self._previous_epoch_detail = -1.
2.2.6 Define Updater¶
We use Backpropagation through time (BPTT) for optimize the RNNLM. BPTT can be implemented by
overriding update_core() method of StandardUpdater. First,
in the constructor of the BPTTUpdater, it takes bprop_len as an argument in addition
to other arguments StandardUpdater needs. bprop_len defines the
length of sequence \(T\) to calculate the loss:
where \(\hat{P}({\bf x}_t^n)\) is a probability for \(n\)-th word in the vocabulary at the position \(t\) in the training data sequence.
class BPTTUpdater(training.updaters.StandardUpdater):
def __init__(self, train_iter, optimizer, bprop_len, device):
super(BPTTUpdater, self).__init__(
train_iter, optimizer, device=device)
self.bprop_len = bprop_len
# The core part of the update routine can be customized by overriding.
def update_core(self):
loss = 0
# When we pass one iterator and optimizer to StandardUpdater.__init__,
# they are automatically named 'main'.
train_iter = self.get_iterator('main')
optimizer = self.get_optimizer('main')
# Progress the dataset iterator for bprop_len words at each iteration.
for i in range(self.bprop_len):
# Get the next batch (a list of tuples of two word IDs)
batch = train_iter.__next__()
# Concatenate the word IDs to matrices and send them to the device
# self.converter does this job
# (it is chainer.dataset.concat_examples by default)
x, t = self.converter(batch, self.device)
# Compute the loss at this time step and accumulate it
loss += optimizer.target(x, t)
optimizer.target.cleargrads() # Clear the parameter gradients
loss.backward() # Backprop
loss.unchain_backward() # Truncate the graph
optimizer.update() # Update the parameters
2.2.7 Define Evaluation Function (Perplexity)¶
Define a function to calculate the perplexity from the loss value. If we take \(e\) as \(b\) in the above definition of perplexity, calculating the perplexity is just to give the loss value to the power of \(e\):
def compute_perplexity(result):
result['perplexity'] = np.exp(result['main/loss'])
if 'validation/main/loss' in result:
result['val_perplexity'] = np.exp(result['validation/main/loss'])
2.2.8 Create Iterator¶
Here, the code below just creates iterator objects from dataset splits (train/val/test).
train_iter = ParallelSequentialIterator(train, args.batchsize)
val_iter = ParallelSequentialIterator(val, 1, repeat=False)
test_iter = ParallelSequentialIterator(test, 1, repeat=False)
2.2.9 Create RNN and Classification Model¶
Instantiate RNNLM model and wrap it with chainer.links.Classifier
because it calculates softmax cross entropy as the loss.
rnn = RNNForLM(n_vocab, args.unit)
model = L.Classifier(rnn)
model.compute_accuracy = False # we only want the perplexity
Note that Classifier computes not only the loss but also accuracy based on a given
input/label pair. To learn the RNN language model, we only need the loss (cross entropy) in the
Classifier because we calculate the perplexity instead of classification accuracy to check
the performance of the model. So, we turn off computing the accuracy by giving False to
model.compute_accuracy attribute.
2.2.10 Setup Optimizer¶
Prepare an optimizer. Here, we use GradientClipping
to prevent gradient explosion. It automatically clips
the gradient to be used to update the parameters in the model with given constant
gradclip.
optimizer = chainer.optimizers.SGD(lr=1.0)
optimizer.setup(model)
optimizer.add_hook(chainer.optimizer_hooks.GradientClipping(args.gradclip))
2.2.11 Setup and Run Trainer¶
Let’s make a trainer object and start the training! Note that we add an
eval_hook to the Evaluator
extension to reset the internal states before starting evaluation process. It can prevent to use
training data during evaluating the model.
updater = BPTTUpdater(train_iter, optimizer, args.bproplen, device)
trainer = training.Trainer(updater, (args.epoch, 'epoch'), out=args.out)
eval_model = model.copy() # Model with shared params and distinct states
eval_rnn = eval_model.predictor
trainer.extend(extensions.Evaluator(
val_iter, eval_model, device=device,
# Reset the RNN state at the beginning of each evaluation
eval_hook=lambda _: eval_rnn.reset_state()))
interval = 10 if args.test else 500
trainer.extend(extensions.LogReport(postprocess=compute_perplexity,
trigger=(interval, 'iteration')))
trainer.extend(extensions.PrintReport(
['epoch', 'iteration', 'perplexity', 'val_perplexity']
), trigger=(interval, 'iteration'))
trainer.extend(extensions.ProgressBar(
update_interval=1 if args.test else 10))
trainer.extend(extensions.snapshot())
trainer.extend(extensions.snapshot_object(
model, 'model_iter_{.updater.iteration}'))
if args.resume is not None:
chainer.serializers.load_npz(args.resume, trainer)
trainer.run()
2.2.12 Evaluate the trained model on test dataset¶
Let’s see the perplexity on the test split. Trainer’s extension can be used as just a normal function
outside of Trainer.
print('test')
eval_rnn.reset_state()
evaluator = extensions.Evaluator(test_iter, eval_model, device=device)
result = evaluator()
print('test perplexity: {}'.format(np.exp(float(result['main/loss']))))
2.3 Run Example¶
2.3.1 Training the model¶
You can train the model with the script: examples/ptb/train_ptb.py
$ pwd
/root2chainer/chainer/examples/ptb
$ python train_ptb.py --test # run by test mode. If you want to use all data, remove "--test".
Downloading from https://raw.githubusercontent.com/wojzaremba/lstm/master/data/ptb.train.txt...
Downloading from https://raw.githubusercontent.com/wojzaremba/lstm/master/data/ptb.valid.txt...
Downloading from https://raw.githubusercontent.com/wojzaremba/lstm/master/data/ptb.test.txt...
#vocab = 10000
test
test perplexity: 29889.9857364
2.3.2 Generating sentences¶
You can generate the sentence which starts with a word in the vocabulary. In this example, we generate a sentence which starts with the word apple. We use the script in the PTB example of the official repository: examples/ptb/gentxt.py
$ pwd
/root2chainer/chainer/examples/ptb
$ python gentxt.py -m model.npz -p apple
apple a new u.s. economist with <unk> <unk> fixed more than to N the company said who is looking back to