Write a Sequence to Sequence (seq2seq) Model¶
0. Introduction¶
The sequence to sequence (seq2seq) model[1][2] is a learning model that converts an input sequence into an output sequence. In this context, the sequence is a list of symbols, corresponding to the words in a sentence. The seq2seq model has achieved great success in fields such as machine translation, dialogue systems, question answering, and text summarization. All of these tasks can be regarded as the task to learn a model that converts an input sequence into an output sequence.
1. Basic Idea of Seq2seq Model¶
1.1 Overview of Seq2seq Model¶
The Notations of Sequence¶
The seq2seq model converts an input sequence into an output sequence. Let the input sequence and the output sequence be \(\bf X\) and \(\bf Y\). The \(i\)-th element of the input sequence is represented as \({\bf x}_i\), and the \(j\)-th element of the output sequence is also represented as \({\bf y}_j\). Generally, each of the \({\bf x}_i\) and the \({\bf y}_j\) is the one-hot vector of the symbols. For example, in natural language processing(NLP), the one-hot vector represents the word and its size becomes the vocabulary size.
Let’s think about the seq2seq model in the context of NLP. Let the vocabulary of the inputs and the outputs be \({\mathcal V}^{(s)}\) and \({\mathcal V}^{(t)}\), all the elements \({\bf x}_i\) and \({\bf y}_j\) satisfy \({\bf x}_i \in \mathbb{R}^{|{\mathcal V}^{(s)}|}\) and \({\bf y}_i \in \mathbb{R}^{|{\mathcal V}^{(t)}|}\). The input sequence \(\bf X\) and the output sequence \(\bf Y\) are represented as the following equations:
\(I\) and \(J\) are the length of the input sequence and the output sequence. Using the typical NLP notation, \({\bf y}_0\) is the one-hot vector of BOS, which is the virtual word representing the beginning of the sentence, and \({\bf y}_{J+1}\) is that of EOS, which is the virtual word representing the end of the sentence.
The Notations of Conditional Probability \(P({\bf Y}|{\bf X})\)¶
Next, let’s think about the conditional probability \(P({\bf Y}|{\bf X})\) generating the output sequence \(\bf Y\) when the input sequence \(\bf X\) is given. The purpose of seq2seq model is modeling the probability \(P({\bf Y}|{\bf X})\). However, the seq2seq model does not model the probability \(P({\bf Y}|{\bf X})\) directly. Actually, it models the probability \(P({\bf y}_j|{\bf Y}_{<j}, {\bf X})\), which is the probability of generating the \(j\)-th element of the output sequence \({\bf y}_j\) given the \({\bf Y}_{<j}\) and \({\bf X}\). \({\bf Y}_{<j}\) means the output sequence from \(1\) to \(j-1\), or \(({\bf y}_j)_{j=1}^{j-1}\). In this notation, you can write the model \(P_{\theta}({\bf Y}|{\bf X})\) with the product of \(P_{\theta}({\bf y}_j|{\bf Y}_{<j}, {\bf X})\):
Processing Steps in Seq2seq Model¶
Now, let’s think about the processing steps in seq2seq model. The feature of seq2seq model is that it consists of the two processes:
The process that generates the fixed size vector \(\bf z\) from the input sequence \(\bf X\)
The process that generates the output sequence \(\bf Y\) from \(\bf z\)
In other words, the information of \(\bf X\) is conveyed by \(\bf z\), and \(P_{\theta}({\bf y}_j|{\bf Y}_{<j}, {\bf X})\) is actually calculated by \(P_{\theta}({\bf y}_j|{\bf Y}_{<j}, {\bf z})\).
First, we represent the process which generating \(\bf z\) from \(\bf X\) by the function \(\Lambda\):
The function \(\Lambda\) may be the recurrent neural net such as LSTMs.
Second, we represent the process which generating \(\bf Y\) from \(\bf z\) by the following formula:
\(\Psi\) is the function to generate the hidden vectors \({\bf h}_j^{(t)}\), and \(\Upsilon\) is the function to calculate the generative probability of the one-hot vector \({\bf y}_j\). When \(j=1\), \({\bf h}_{j-1}^{(t)}\) or \({\bf h}_0^{(t)}\) is \(\bf z\) generated by \(\Lambda({\bf X})\), and \({\bf y}_{j-1}\) or \({\bf y}_0\) is the one-hot vector of BOS.
1.2 Model Architecture of Seq2seq Model¶
In this section, we describe the architecture of seq2seq model. To simplify the explanation, we use the most basic architecture. The architecture of seq2seq model can be separated to the five major roles.
Encoder Embedding Layer
Encoder Recurrent Layer
Decoder Embedding Layer
Decoder Recurrent Layer
Decoder Output Layer
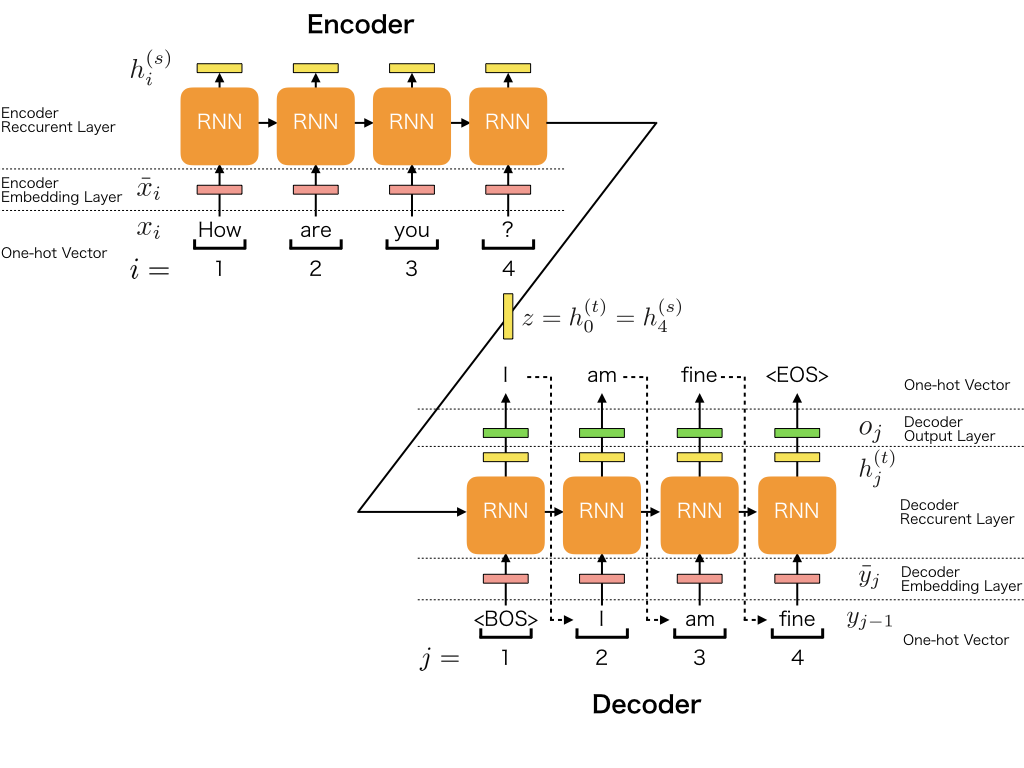
The encoder consists of two layers: the embedding layer and the recurrent layer, and the decoder consists of three layers: the embedding layer, the recurrent layer, and the output layer.
In the explanation, we use the following symbols:
Symbol |
Definition |
|---|---|
\(H\) |
the size of the hidden vector |
\(D\) |
the size of the embedding vector |
\({\bf x}_i\) |
the one-hot vector of \(i\)-th word in the input sentence |
\({\bf \bar x}_i\) |
the embedding vector of \(i\)-th word in the input sentence |
\({\bf E}^{(s)}\) |
Embedding matrix of the encoder |
\({\bf h}_i^{(s)}\) |
the \(i\)-th hidden vector of the encoder |
\({\bf y}_j\) |
the one-hot vector of \(j\)-th word in the output sentence |
\({\bf \bar y}_j\) |
the embedding vector of \(j\)-th word in the output sentence |
\({\bf E}^{(t)}\) |
Embedding matrix of the decoder |
\({\bf h}_j^{(t)}\) |
the \(j\)-th hidden vector of the decoder |
1.2.1 Encoder Embedding Layer¶
The first layer, or the encoder embedding layer converts the each word in the input sentence to the embedding vector. When processing the \(i\)-th word in the input sentence, the input and the output of the layer are the following:
The input is \({\bf x}_i\) : the one-hot vector which represents \(i\)-th word
The output is \({\bf \bar x}_i\) : the embedding vector which represents \(i\)-th word
Each embedding vector is calculated by the following equation:
\({\bf E}^{(s)} \in {\mathbb R}^{D \times |{\mathcal V}^{(s)}|}\) is the embedding matrix of the encoder.
1.2.2 Encoder Recurrent Layer¶
The encoder recurrent layer generates the hidden vectors from the embedding vectors. When processing the \(i\)-th embedding vector, the input and the output of the layer are the following:
The input is \({\bf \bar x}_i\) : the embedding vector which represents the \(i\)-th word
The output is \({\bf h}_i^{(s)}\) : the hidden vector of the \(i\)-th position
For example, when using the uni-directional RNN of one layer, the process can be represented as the following function \(\Psi^{(s)}\):
In this case, we use the \({\rm tanh}\) as the activation function.
1.2.3 Decoder Embedding Layer¶
The decoder embedding layer converts the each word in the output sentence to the embedding vector. When processing the \(j\)-th word in the output sentence, the input and the output of the layer are the following:
The input is \({\bf y}_{j-1}\) : the one-hot vector which represents the \((j-1)\)-th word generated by the decoder output layer
The output is \({\bf \bar y}_j\) : the embedding vector which represents the \((j-1)\)-th word
Each embedding vector is calculated by the following equation:
\({\bf E}^{(t)} \in {\mathbb R}^{D \times |{\mathcal V}^{(t)}|}\) is the embedding matrix of the encoder.
1.2.4 Decoder Recurrent Layer¶
The decoder recurrent layer generates the hidden vectors from the embedding vectors. When processing the \(j\)-th embedding vector, the input and the output of the layer are the following:
The input is \({\bf \bar y}_j\) : the embedding vector
The output is \({\bf h}_j^{(t)}\) : the hidden vector of \(j\)-th position
For example, when using the uni-directional RNN of one layer, the process can be represented as the following function \(\Psi^{(t)}\):
In this case, we use the \({\rm tanh}\) as the activation function. And we must use the encoder’s hidden vector of the last position as the decoder’s hidden vector of first position as following:
1.2.5 Decoder Output Layer¶
The decoder output layer generates the probability of the \(j\)-th word of the output sentence from the hidden vector. When processing the \(j\)-th embedding vector, the input and the output of the layer are the following:
The input is \({\bf h}_j^{(t)}\) : the hidden vector of \(j\)-th position
The output is \(p_j\) : the probability of generating the one-hot vector \({\bf y}_j\) of the \(j\)-th word
Note
There are a lot of varieties of seq2seq models. We can use the different RNN models in terms of: (1) directionality (unidirectional or bidirectional), (2) depth (single-layer or multi-layer), (3) type (a vanilla RNN, a Long Short-term Memory (LSTM), or a gated recurrent unit (GRU)), and (4) additional functionality (s.t. Attention Mechanism).
2. Implementation of Seq2seq Model¶
The official Chainer repository includes a neural machine translation example using the seq2seq model. We will now provide an overview of the example and explain its implementation in detail. chainer/examples/seq2seq
2.1 Model Overview¶
In this simple example, an input sequence is processed by a stacked LSTM-RNN (long short-term memory recurrent neural networks) and it is encoded as a fixed-size vector. The output sequence is also processed by another stacked LSTM-RNN. At decoding time, an output sequence is generated using argmax.
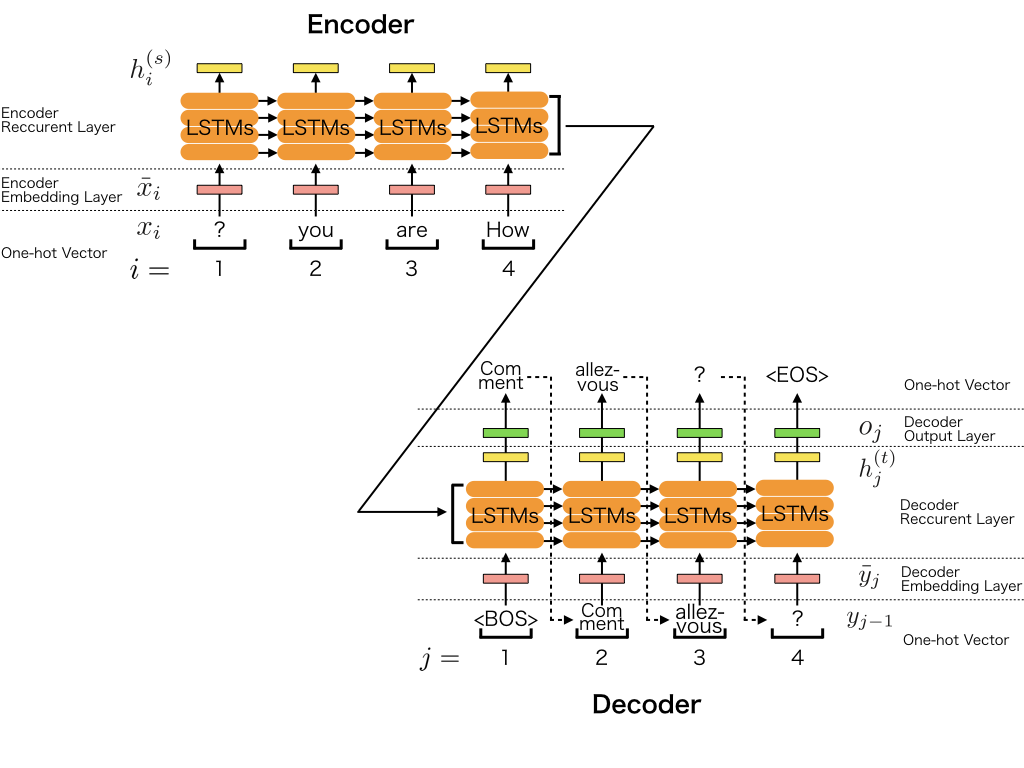
2.2 Step-by-step Implementation¶
2.2.1 Import Package¶
First, let’s import necessary packages.
import io
from nltk.translate import bleu_score
import numpy
import progressbar
import six
import chainer
import chainer.functions as F
import chainer.links as L
from chainer import training
2.2.2 Define Training Settings¶
Define all training settings here.
parser.add_argument('SOURCE', help='source sentence list')
parser.add_argument('TARGET', help='target sentence list')
parser.add_argument('SOURCE_VOCAB', help='source vocabulary file')
parser.add_argument('TARGET_VOCAB', help='target vocabulary file')
parser.add_argument('--validation-source',
help='source sentence list for validation')
parser.add_argument('--validation-target',
help='target sentence list for validation')
parser.add_argument('--batchsize', '-b', type=int, default=64,
help='number of sentence pairs in each mini-batch')
parser.add_argument('--epoch', '-e', type=int, default=20,
help='number of sweeps over the dataset to train')
parser.add_argument('--resume', '-r', type=str,
help='resume the training from snapshot')
parser.add_argument('--save', '-s', type=str,
help='save a snapshot of the training')
parser.add_argument('--unit', '-u', type=int, default=1024,
help='number of units')
parser.add_argument('--layer', '-l', type=int, default=3,
help='number of layers')
parser.add_argument('--use-dataset-api', default=False,
action='store_true',
help='use TextDataset API to reduce CPU memory usage')
parser.add_argument('--min-source-sentence', type=int, default=1,
help='minimium length of source sentence')
parser.add_argument('--max-source-sentence', type=int, default=50,
help='maximum length of source sentence')
parser.add_argument('--min-target-sentence', type=int, default=1,
help='minimium length of target sentence')
parser.add_argument('--max-target-sentence', type=int, default=50,
help='maximum length of target sentence')
parser.add_argument('--log-interval', type=int, default=200,
help='number of iteration to show log')
parser.add_argument('--validation-interval', type=int, default=4000,
help='number of iteration to evlauate the model '
'with validation dataset')
parser.add_argument('--device', '-d', type=str, default='-1',
help='Device specifier. Either ChainerX device '
'specifier or an integer. If non-negative integer, '
'CuPy arrays with specified device id are used. If '
'negative integer, NumPy arrays are used')
parser.add_argument('--out', '-o', default='result',
help='directory to output the result')
group = parser.add_argument_group('deprecated arguments')
group.add_argument('--gpu', '-g', dest='device',
type=int, nargs='?', const=0,
help='GPU ID (negative value indicates CPU)')
2.2.3 Define Network Structure¶
The Chainer implementation of seq2seq is shown below. It implements the model depicted in the above figure.
class Seq2seq(chainer.Chain):
def __init__(self, n_layers, n_source_vocab, n_target_vocab, n_units):
super(Seq2seq, self).__init__()
with self.init_scope():
self.embed_x = L.EmbedID(n_source_vocab, n_units)
self.embed_y = L.EmbedID(n_target_vocab, n_units)
self.encoder = L.NStepLSTM(n_layers, n_units, n_units, 0.1)
self.decoder = L.NStepLSTM(n_layers, n_units, n_units, 0.1)
self.W = L.Linear(n_units, n_target_vocab)
self.n_layers = n_layers
self.n_units = n_units
def forward(self, xs, ys):
xs = [x[::-1] for x in xs]
eos = self.xp.array([EOS], numpy.int32)
ys_in = [F.concat([eos, y], axis=0) for y in ys]
ys_out = [F.concat([y, eos], axis=0) for y in ys]
# Both xs and ys_in are lists of arrays.
exs = sequence_embed(self.embed_x, xs)
eys = sequence_embed(self.embed_y, ys_in)
batch = len(xs)
# None represents a zero vector in an encoder.
hx, cx, _ = self.encoder(None, None, exs)
_, _, os = self.decoder(hx, cx, eys)
# It is faster to concatenate data before calculating loss
# because only one matrix multiplication is called.
concat_os = F.concat(os, axis=0)
concat_ys_out = F.concat(ys_out, axis=0)
loss = F.sum(F.softmax_cross_entropy(
self.W(concat_os), concat_ys_out, reduce='no')) / batch
chainer.report({'loss': loss}, self)
n_words = concat_ys_out.shape[0]
perp = self.xp.exp(loss.array * batch / n_words)
chainer.report({'perp': perp}, self)
return loss
def translate(self, xs, max_length=100):
batch = len(xs)
with chainer.no_backprop_mode(), chainer.using_config('train', False):
xs = [x[::-1] for x in xs]
exs = sequence_embed(self.embed_x, xs)
h, c, _ = self.encoder(None, None, exs)
ys = self.xp.full(batch, EOS, numpy.int32)
result = []
for i in range(max_length):
eys = self.embed_y(ys)
eys = F.split_axis(eys, batch, 0)
h, c, ys = self.decoder(h, c, eys)
cys = F.concat(ys, axis=0)
wy = self.W(cys)
ys = self.xp.argmax(wy.array, axis=1).astype(numpy.int32)
result.append(ys)
# Using `xp.concatenate(...)` instead of `xp.stack(result)` here to
# support NumPy 1.9.
result = chainer.get_device('@numpy').send(
self.xp.concatenate([x[None, :] for x in result]).T)
# Remove EOS taggs
outs = []
for y in result:
inds = numpy.argwhere(y == EOS)
if len(inds) > 0:
y = y[:inds[0, 0]]
outs.append(y)
return outs
In
Seq2seq, three functions are defined: the constructor__init__, the function callforward, and the function for translationtranslate.
def __init__(self, n_layers, n_source_vocab, n_target_vocab, n_units):
super(Seq2seq, self).__init__()
with self.init_scope():
self.embed_x = L.EmbedID(n_source_vocab, n_units)
self.embed_y = L.EmbedID(n_target_vocab, n_units)
self.encoder = L.NStepLSTM(n_layers, n_units, n_units, 0.1)
self.decoder = L.NStepLSTM(n_layers, n_units, n_units, 0.1)
self.W = L.Linear(n_units, n_target_vocab)
self.n_layers = n_layers
self.n_units = n_units
When we instantiate this class for making a model, we give the number of stacked lstms to
n_layers, the vocabulary size of the source language ton_source_vocab, the vocabulary size of the target language ton_target_vocab, and the size of hidden vectors ton_units.This network uses
chainer.links.NStepLSTM,chainer.links.EmbedID, andchainer.links.Linearas its building blocks. All the layers are registered and initialized in the context withself.init_scope().You can access all the parameters in those layers by calling
self.params().In the constructor, it initializes all parameters with values sampled from a uniform distribution \(U(-1, 1)\).
def forward(self, xs, ys):
xs = [x[::-1] for x in xs]
eos = self.xp.array([EOS], numpy.int32)
ys_in = [F.concat([eos, y], axis=0) for y in ys]
ys_out = [F.concat([y, eos], axis=0) for y in ys]
# Both xs and ys_in are lists of arrays.
exs = sequence_embed(self.embed_x, xs)
eys = sequence_embed(self.embed_y, ys_in)
batch = len(xs)
# None represents a zero vector in an encoder.
hx, cx, _ = self.encoder(None, None, exs)
_, _, os = self.decoder(hx, cx, eys)
# It is faster to concatenate data before calculating loss
# because only one matrix multiplication is called.
concat_os = F.concat(os, axis=0)
concat_ys_out = F.concat(ys_out, axis=0)
loss = F.sum(F.softmax_cross_entropy(
self.W(concat_os), concat_ys_out, reduce='no')) / batch
chainer.report({'loss': loss}, self)
n_words = concat_ys_out.shape[0]
perp = self.xp.exp(loss.array * batch / n_words)
chainer.report({'perp': perp}, self)
return loss
The
forwardmethod takes sequences of source language’s word IDsxsand sequences of target language’s word IDsys. Each sequence represents a sentence, and the size ofxsis mini-batch size.Note that the sequences of word IDs
xsandysare converted to a vocabulary-size one-hot vectors and then multiplied with the embedding matrix insequence_embedto obtain embedding vectorsexsandeys.seq2seq.py¶def sequence_embed(embed, xs): x_len = [len(x) for x in xs] x_section = numpy.cumsum(x_len[:-1]) ex = embed(F.concat(xs, axis=0)) exs = F.split_axis(ex, x_section, 0) return exs
self.encoderandself.decoderare the encoder and the decoder of the seq2seq model. Each element of the decoder outputosis \(h_{[1:J]}^{(t)}\) in the figure above.After calculating the recurrent layer output, the loss
lossand the perplexityperpare calculated, and the values are logged bychainer.report.
Note
It is well known that the seq2seq model learns much better when the source
sentences are reversed.
The paper[1] says that “While the LSTM is capable of solving problems with
long term dependencies, we discovered that the LSTM learns much better when
the source sentences are reversed (the target sentences are not reversed).
By doing so, the LSTM’s test perplexity dropped from 5.8 to 4.7, and the test
BLEU scores of its decoded translations increased from 25.9 to 30.6.”
So, at the first line in the forward, the input sentences are reversed
xs = [x[::-1] for x in xs].
def translate(self, xs, max_length=100):
batch = len(xs)
with chainer.no_backprop_mode(), chainer.using_config('train', False):
xs = [x[::-1] for x in xs]
exs = sequence_embed(self.embed_x, xs)
h, c, _ = self.encoder(None, None, exs)
ys = self.xp.full(batch, EOS, numpy.int32)
result = []
for i in range(max_length):
eys = self.embed_y(ys)
eys = F.split_axis(eys, batch, 0)
h, c, ys = self.decoder(h, c, eys)
cys = F.concat(ys, axis=0)
wy = self.W(cys)
ys = self.xp.argmax(wy.array, axis=1).astype(numpy.int32)
result.append(ys)
# Using `xp.concatenate(...)` instead of `xp.stack(result)` here to
# support NumPy 1.9.
result = chainer.get_device('@numpy').send(
self.xp.concatenate([x[None, :] for x in result]).T)
# Remove EOS taggs
outs = []
for y in result:
inds = numpy.argwhere(y == EOS)
if len(inds) > 0:
y = y[:inds[0, 0]]
outs.append(y)
return outs
After the model learned the parameters, the function
translateis called to generate the translated sentencesoutsfrom the source sentencesxs.So as not to change the parameters, the codes for the translation are nested in the scope
chainer.no_backprop_mode()andchainer.using_config('train', False).
2.2.4 Load French-English Corpus from WMT15 Dataset¶
In this tutorial, we use French-English corpus from WMT15 website that contains 10^9 documents. We must prepare additional libraries, dataset, and parallel corpus. To understand the pre-processing, see 2.3.1 Requirements.
After the pre-processing the dataset, let’s make dataset objects:
# Load pre-processed dataset
print('[{}] Loading dataset... (this may take several minutes)'.format(
datetime.datetime.now()))
source_ids = load_vocabulary(args.SOURCE_VOCAB)
target_ids = load_vocabulary(args.TARGET_VOCAB)
if args.use_dataset_api:
# By using TextDataset, you can avoid loading whole dataset on memory.
# This significantly reduces the host memory usage.
def _filter_func(s, t):
sl = len(s.strip().split()) # number of words in source line
tl = len(t.strip().split()) # number of words in target line
return (
args.min_source_sentence <= sl <= args.max_source_sentence and
args.min_target_sentence <= tl <= args.max_target_sentence)
train_data = load_data_using_dataset_api(
source_ids, args.SOURCE,
target_ids, args.TARGET,
_filter_func,
)
else:
# Load all records on memory.
train_source = load_data(source_ids, args.SOURCE)
train_target = load_data(target_ids, args.TARGET)
assert len(train_source) == len(train_target)
train_data = [
(s, t)
for s, t in six.moves.zip(train_source, train_target)
if (args.min_source_sentence <= len(s) <= args.max_source_sentence
and
args.min_target_sentence <= len(t) <= args.max_target_sentence)
]
print('[{}] Dataset loaded.'.format(datetime.datetime.now()))
if not args.use_dataset_api:
# Skip printing statistics when using TextDataset API, as it is slow.
train_source_unknown = calculate_unknown_ratio(
[s for s, _ in train_data])
train_target_unknown = calculate_unknown_ratio(
[t for _, t in train_data])
print('Source vocabulary size: %d' % len(source_ids))
print('Target vocabulary size: %d' % len(target_ids))
print('Train data size: %d' % len(train_data))
print('Train source unknown ratio: %.2f%%' % (
train_source_unknown * 100))
print('Train target unknown ratio: %.2f%%' % (
train_target_unknown * 100))
target_words = {i: w for w, i in target_ids.items()}
source_words = {i: w for w, i in source_ids.items()}
This code uses utility functions below:
seq2seq.py¶def load_vocabulary(path): with io.open(path, encoding='utf-8') as f: # +2 for UNK and EOS word_ids = {line.strip(): i + 2 for i, line in enumerate(f)} word_ids['<UNK>'] = 0 word_ids['<EOS>'] = 1 return word_ids
seq2seq.py¶def load_data(vocabulary, path): n_lines = count_lines(path) bar = progressbar.ProgressBar() data = [] print('loading...: %s' % path) with io.open(path, encoding='utf-8') as f: for line in bar(f, max_value=n_lines): words = line.strip().split() array = numpy.array([vocabulary.get(w, UNK) for w in words], numpy.int32) data.append(array) return data
seq2seq.py¶def calculate_unknown_ratio(data): unknown = sum((s == UNK).sum() for s in data) total = sum(s.size for s in data) return unknown / total
2.2.5 Define Evaluation Function (Bleu Score)¶
BLEU[3] (bilingual evaluation understudy) is the evaluation metric for the quality of text which has been machine-translated from one natural language to another.
class CalculateBleu(chainer.training.Extension):
trigger = 1, 'epoch'
priority = chainer.training.PRIORITY_WRITER
def __init__(
self, model, test_data, key, device, batch=100, max_length=100):
self.model = model
self.test_data = test_data
self.key = key
self.batch = batch
self.device = device
self.max_length = max_length
def __call__(self, trainer):
device = self.device
with chainer.no_backprop_mode():
references = []
hypotheses = []
for i in range(0, len(self.test_data), self.batch):
sources, targets = zip(*self.test_data[i:i + self.batch])
references.extend([[t.tolist()] for t in targets])
sources = [device.send(x) for x in sources]
ys = [y.tolist()
for y in self.model.translate(sources, self.max_length)]
hypotheses.extend(ys)
bleu = bleu_score.corpus_bleu(
references, hypotheses,
smoothing_function=bleu_score.SmoothingFunction().method1)
chainer.report({self.key: bleu})
2.2.6 Create Iterator¶
Here, the code below just creates iterator objects.
train_iter = chainer.iterators.SerialIterator(train_data, args.batchsize)
2.2.7 Create RNN and Classification Model¶
Instantiate Seq2seq model.
model = Seq2seq(args.layer, len(source_ids), len(target_ids), args.unit)
2.2.8 Setup Optimizer¶
Prepare an optimizer. We use chainer.optimizers.Adam.
optimizer = chainer.optimizers.Adam()
optimizer.setup(model)
2.2.9 Setup and Run Trainer¶
Let’s make a trainer object.
updater = training.updaters.StandardUpdater(
train_iter, optimizer, converter=convert, device=device)
trainer = training.Trainer(updater, (args.epoch, 'epoch'), out=args.out)
trainer.extend(extensions.LogReport(
trigger=(args.log_interval, 'iteration')))
trainer.extend(extensions.PrintReport(
['epoch', 'iteration', 'main/loss', 'main/perp',
'validation/main/bleu', 'elapsed_time']),
trigger=(args.log_interval, 'iteration'))
trainer.extend(
extensions.snapshot(filename='snapshot_epoch_{.updater.iteration}'),
trigger=(args.validation_interval, 'iteration'))
Setup the trainer’s extension to see the BLEU score on the test data.
test_source = load_data(source_ids, args.validation_source)
test_target = load_data(target_ids, args.validation_target)
assert len(test_source) == len(test_target)
test_data = list(six.moves.zip(test_source, test_target))
test_data = [(s, t) for s, t in test_data if 0 < len(s) and 0 < len(t)]
test_source_unknown = calculate_unknown_ratio(
[s for s, _ in test_data])
test_target_unknown = calculate_unknown_ratio(
[t for _, t in test_data])
print('Validation data: %d' % len(test_data))
print('Validation source unknown ratio: %.2f%%' %
(test_source_unknown * 100))
print('Validation target unknown ratio: %.2f%%' %
(test_target_unknown * 100))
@chainer.training.make_extension()
def translate(trainer):
source, target = test_data[numpy.random.choice(len(test_data))]
result = model.translate([model.xp.array(source)])[0]
source_sentence = ' '.join([source_words[x] for x in source])
target_sentence = ' '.join([target_words[y] for y in target])
result_sentence = ' '.join([target_words[y] for y in result])
print('# source : ' + source_sentence)
print('# result : ' + result_sentence)
print('# expect : ' + target_sentence)
trainer.extend(
translate, trigger=(args.validation_interval, 'iteration'))
trainer.extend(
CalculateBleu(
model, test_data, 'validation/main/bleu', device),
trigger=(args.validation_interval, 'iteration'))
if args.resume is not None:
# Resume from a snapshot
chainer.serializers.load_npz(args.resume, trainer)
Let’s start the training!
trainer.run()
if args.save is not None:
# Save a snapshot
chainer.serializers.save_npz(args.save, trainer)
2.3 Run Example¶
2.3.1 Requirements¶
Before running the example, you must prepare additional libraries, dataset, and parallel corpus.
See the detail description: chainer/examples/seq2seq/README.md
2.3.1 Training the model¶
You can train the model with the script: chainer/examples/seq2seq/seq2seq.py
$ pwd
/root2chainer/chainer/examples/seq2seq
$ python seq2seq.py --gpu=0 giga-fren.preprocess.en giga-fren.preprocess.fr \
vocab.en vocab.fr \
--validation-source newstest2013.preprocess.en \
--validation-target newstest2013.preprocess.fr > log
100% (22520376 of 22520376) |#############| Elapsed Time: 0:09:20 Time: 0:09:20
100% (22520376 of 22520376) |#############| Elapsed Time: 0:10:36 Time: 0:10:36
100% (3000 of 3000) |#####################| Elapsed Time: 0:00:00 Time: 0:00:00
100% (3000 of 3000) |#####################| Elapsed Time: 0:00:00 Time: 0:00:00
epoch iteration main/loss validation/main/loss main/perp validation/main/perp validation/main/bleu elapsed_time
0 200 171.449 991.556 85.6739
0 400 143.918 183.594 172.473
0 600 133.48 126.945 260.315
0 800 128.734 104.127 348.062
0 1000 124.741 91.5988 436.536
...
Note
Before running the script, be careful the locale and the python’s encoding. Please setup them to use utf-8 encoding.
2.3.1 Validate the model¶
While you are training the model, you can get the validation results:
...
# source : We knew the Government had tried many things , like launching <UNK> with <UNK> or organising speed dating evenings .
# result : Nous savions que le gouvernement avait <UNK> plusieurs fois , comme le <UNK> <UNK> , le <UNK> ou le <UNK> <UNK> .
# expect : Nous savions que le gouvernement avait tenté plusieurs choses comme lancer des parfums aux <UNK> ou organiser des soirées de <UNK>
...