Model Parallel on ChainerMN¶
Step 1: Communicators¶
To perform multi-node communications, a communicator is needed. Basic usages are the same with the case of the data parallel, see Step 1: Communicators and Optimizers:
comm = chainermn.create_communicator()
If you want to define collective communications among limited number of processes later, it is useful to split the communicator:
subcomm = comm.split(comm.rank % 2, comm.rank)
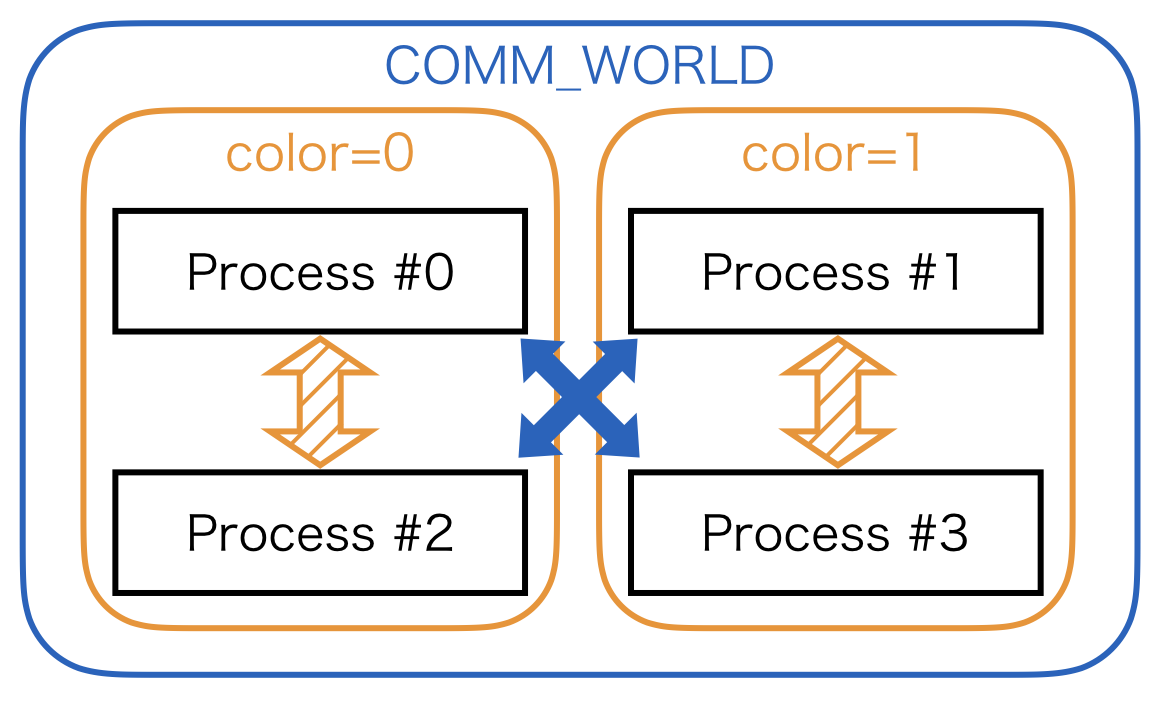
For further detail about the communicator split, please refer to MPI tutorial.
Step 2: Datasets and Iterators¶
In model parallel training, all processes belong to at least one of the following dataset input patterns.
model inputs come from datasets, and each process takes different mini-batches
model inputs come from datasets, and several processes share the same mini-batches
model inputs come from other processes
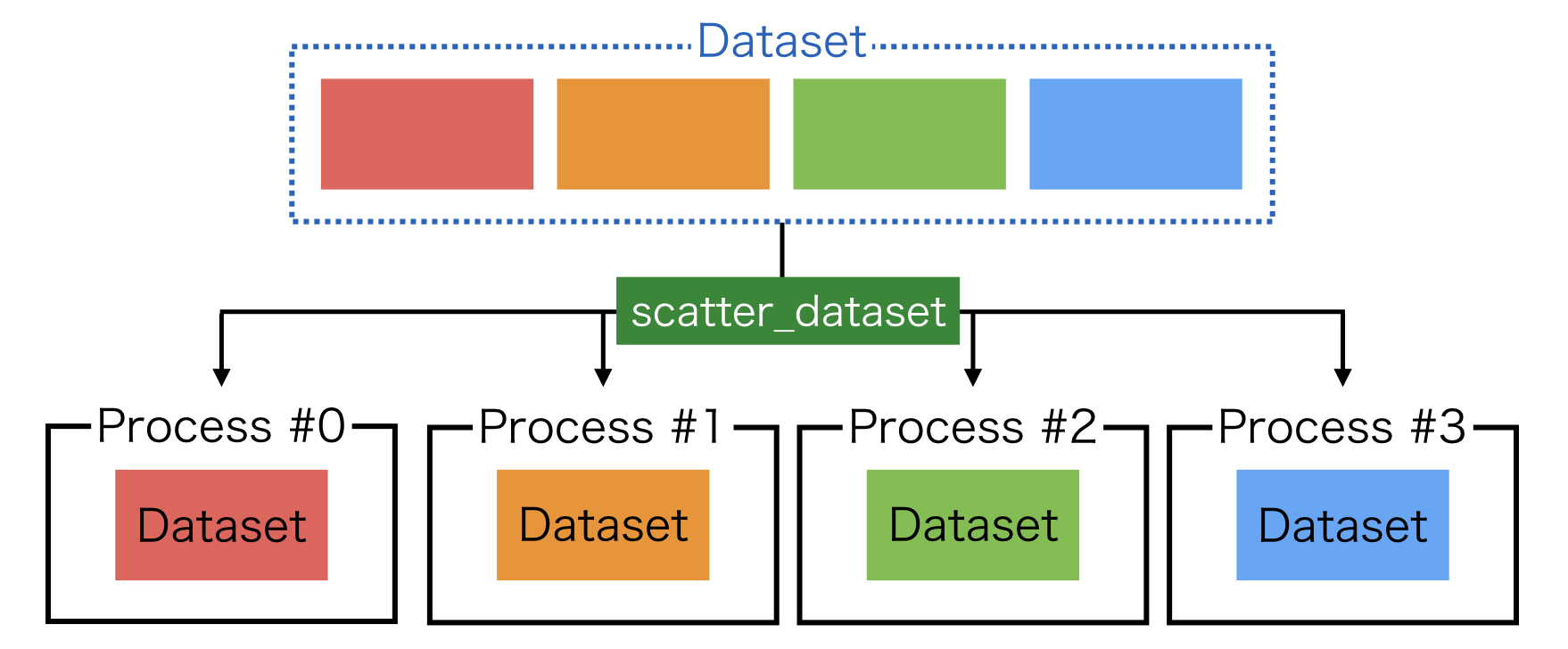
1. scatter_dataset¶
For the first case, you may use scatter_dataset as is introduced in Step 2: Datasets and Evaluators.
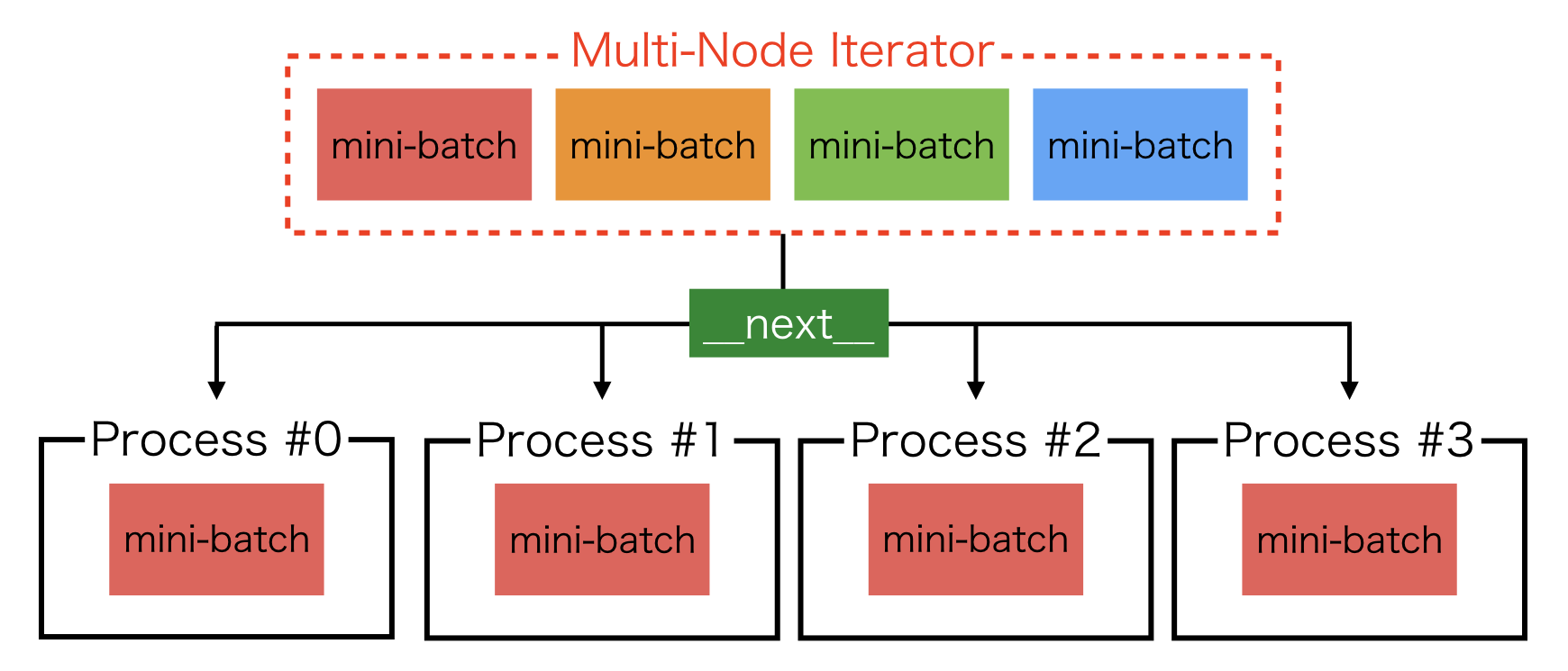
2. multi node iterator¶
For the second case, iterator need to be modified, where create_multi_node_iterator is useful:
train, test = chainer.datasets.get_mnist()
train_iter = chainermn.iterators.create_multi_node_iterator(
chainer.iterators.SerialIterator(train, batchsize), comm)
test_iter = chainermn.iterators.create_multi_node_iterator(
chainer.iterators.SerialIterator(test, batchsize), comm)
The resulting iterators return the same mini-batches among processes specified by the communicator.
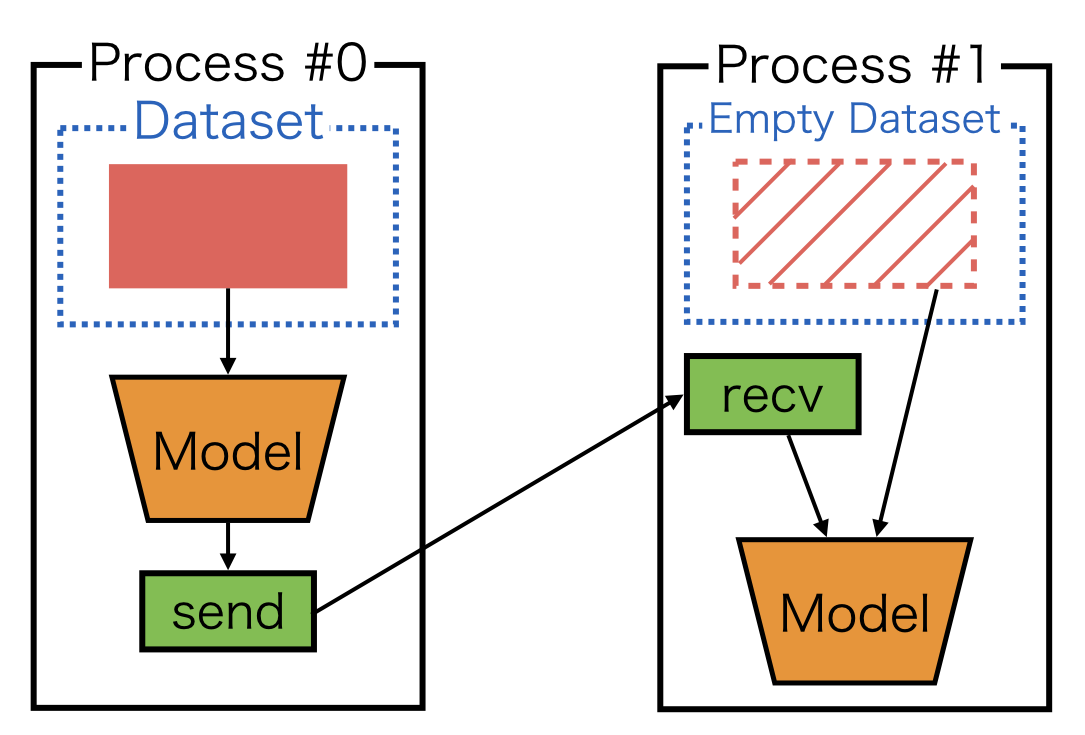
3. empty dataset¶
For the last case, you may use create_empty_dataset, which returns a dataset with the same number of empty tuples as the original dataset:
train, test = chainer.datasets.get_mnist()
train = chainermn.datasets.create_empty_dataset(train)
test = chainermn.datasets.create_empty_dataset(test)
This input pattern appears in the subsequent examples such as Example 1: Simple MLP. Note that datasets are required in Chainer’s updater API. The empty dataset can be used as a dummy dataset.
Step 3: Define Communications¶
ChainerMN supports most of the MPI communications as Chainer functions, including point-to-point and collective communications. To know usages of each communication, please refer to API Reference.
Example 1: Point-to-point Communication¶
This is an example to use point-to-point communications:
def __call__(self, x):
h = f(x)
h = chainermn.functions.send(x, comm, rank=1)
return h
The communication target is specified by rank parameter.
Note that the return value of send is often not negligible.
Please refer to Note: Define-by-Run and Model Parallelism.
Example 2: Collective Communication¶
Here is another example to use collective communications:
def __call__(self, x):
h = f(x)
h = chainermn.functions.allgather(comm, h)
h = F.stack(h, axis=0)
h = F.average(h, axis=0)
return h
This pattern often appears in the averaging ensemble training.
Note: Define-by-Run and Model Parallelism¶
In model-parallel training, a model on each process may become non-connected computational graph. Let’s take a look at an example.

Naive implementation of a model on process #0 could be:
class Model_0(chainer.Chain):
def __call__(self, x):
# first component
z = f(x)
chainermn.functions.send(z, comm, rank=1)
# second component
z = chainermn.functions.recv(comm, rank=1)
y = h(z)
return y
One may notice that there is no connection between the first and second components of computational graph.
As we rely on defined-by-run framework, we cannot build a backward path from the second component to the first component.
In order to build the backward path, a dummy variable, which we call delegate_variable, is needed.
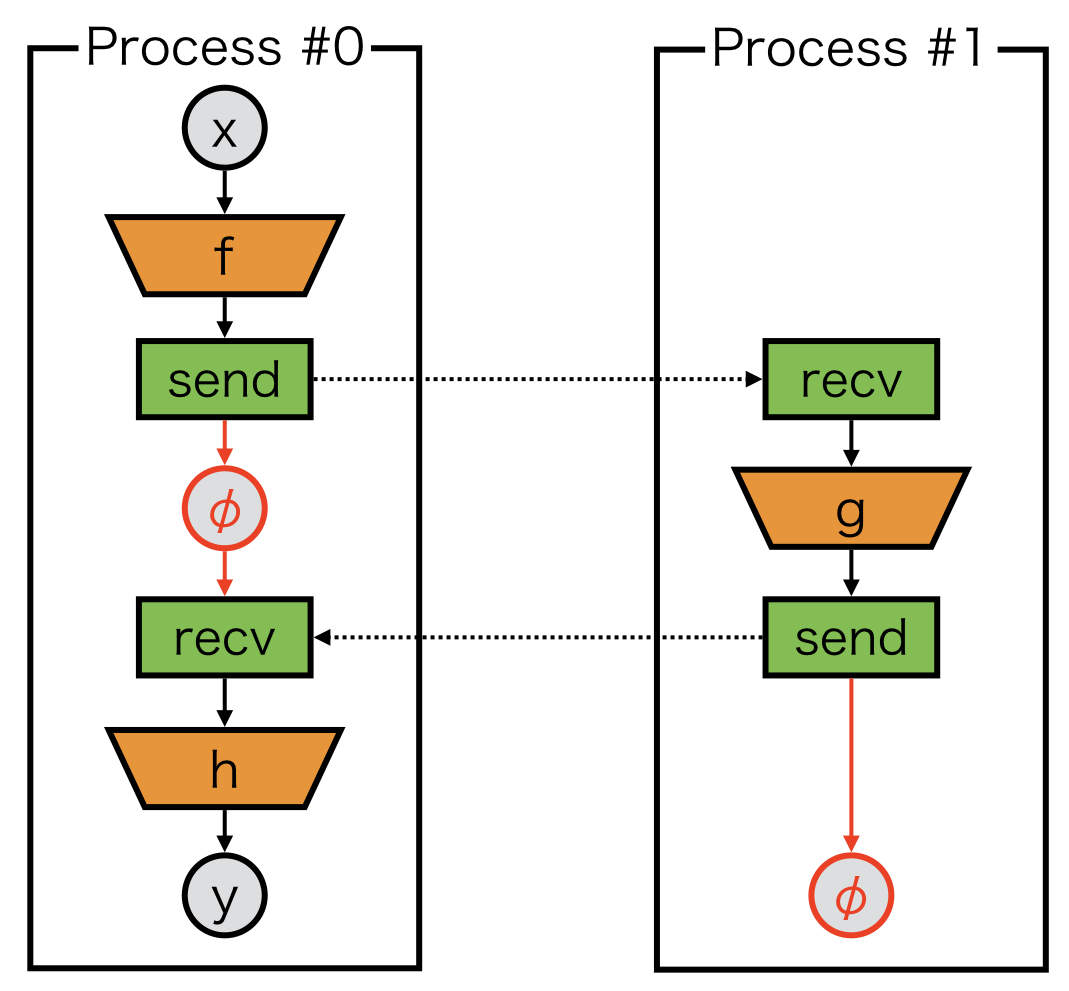
The variable \(\phi\) in the above figure is delegate_variable, which is a return value of send and passed to an argument of recv:
class Model_0(chainer.Chain):
def __call__(self, x):
# first component
z = f(x)
phi = chainermn.functions.send(z, comm, rank=1)
# second component
z = chainermn.functions.recv(comm, rank=1, delegate_variable=phi)
y = h(z)
return y
class Model_1(chainer.Chain):
def __call__(self, _):
z = chainermn.functions.recv(comm, rank=0)
z = g(z)
phi = chainermn.functions.send(z, comm, rank=0)
return phi
Model_1 also need to return a delegate variable \(\phi\) to backtrack its computational graph to compute gradients.
Thus, the backward computation is guaranteed.
Otherwise, backward computation will cause deadlock.
Note: Delegate Variable and Pseudo Connect¶
As we just see above, delegate variables must be appropriately handled to avoid potential deadlock.
However, there are still some pathological cases.
Let’s consider to send variables twice.
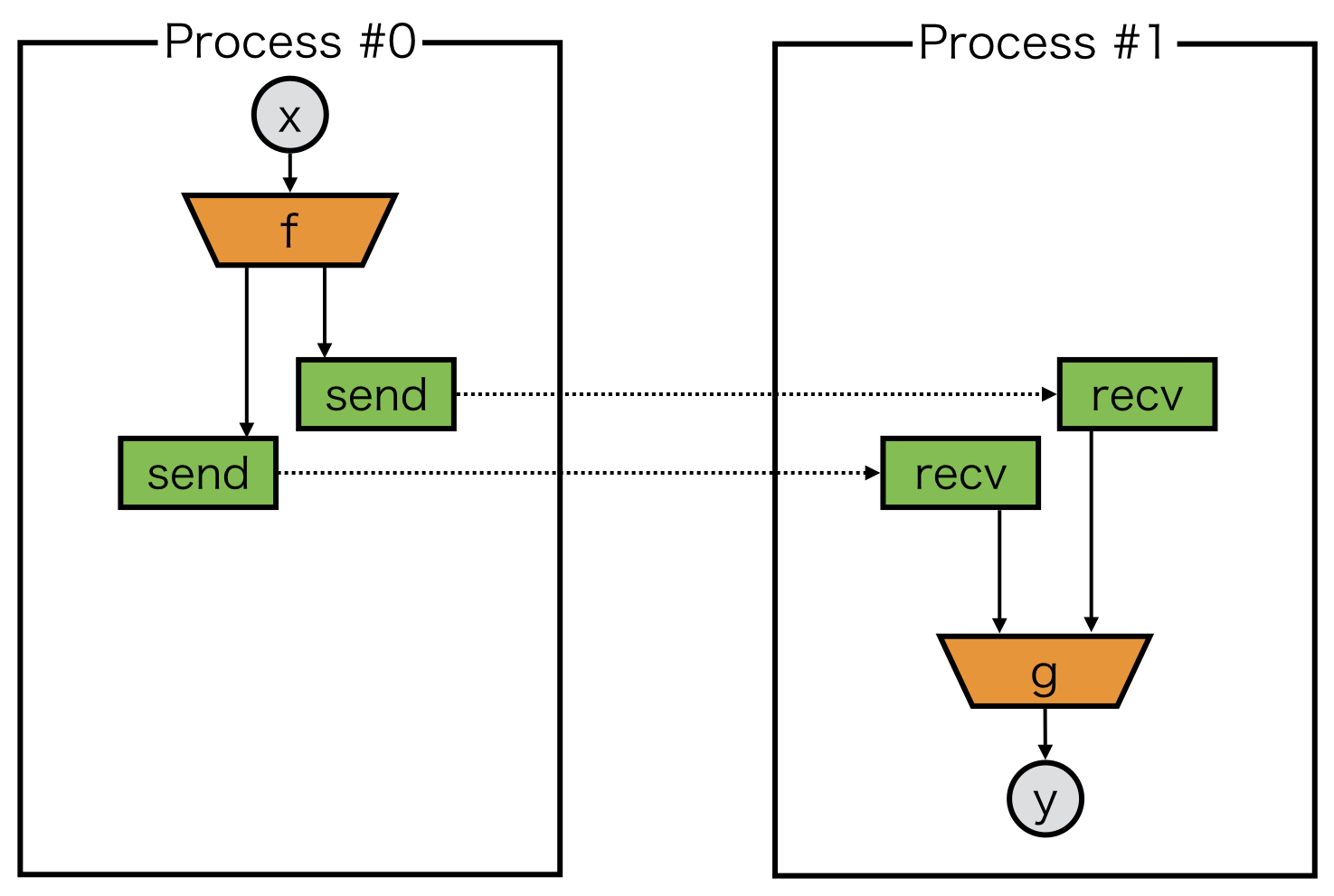
Here, we must guarantee that backward tracking can find two send, but we can only return one delegate variable from each model.
pseudo_connect is a special function to combine one delegate variable to another variable.
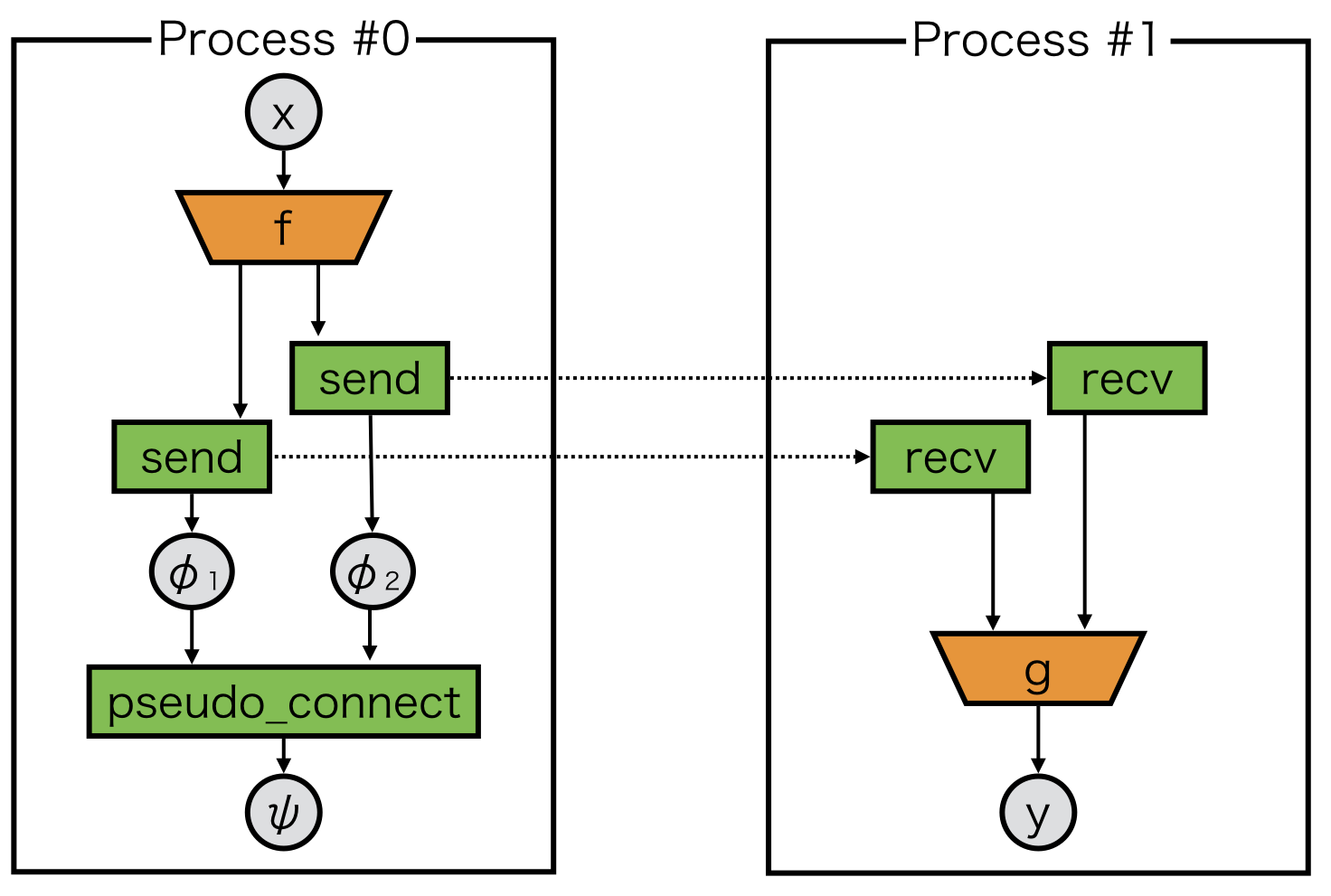
In the above case, the returned variable \(\psi\) from pseudo_connect behaves as if it is \(\phi_2\), while its backward backtracks both \(\phi_1\) and \(\phi_2\):
class Model_0(chainer.Chain):
def __call__(self, x):
z1, z2 = f(x)
phi1 = chainermn.functions.send(z1, comm, rank=1)
phi2 = chainermn.functions.send(z2, comm, rank=1)
psi = chainermn.functions.pseudo_connect(phi1, phi2)
return psi
class Model_1(chainer.Chain):
def __call__(self, _):
z1 = chainermn.functions.recv(comm, rank=0)
z2 = chainermn.functions.recv(comm, rank=0)
y = g(z1, z2)
return y